こんにちは!
1級FP技能士のアシまるくんです!
前編はたくさんのリアクションをいただき、誠にありがとうございます。
大変励みになり、心から嬉しく思います。では、後編をどうぞ。
第4章『算数っていったい何なのさ』
さて、小学校で習う"算数"が、中学校に上がった途端、”数学”に名前を変えます。
いったい何が違うのでしょうか?
よくある答えとしては、『数学には"証明"がある。』ですね。まあ、これについては部分的に賛成です。あと、もう一つ思いつくのは、『算数は"具体的"、数学は"抽象的"である。』ですね。これは、さっきの回答よりもいいかもしれません。
しかし、皆様、中学校に上がりたての頃を思い出してください。数学に変わって初めに習うのは"正負の数"(*1)ではありませんでしたか?そして、思いませんでしたか?
『2-3はマイナス1です。』と言われ、『そんな簡単なこと、算数で教えてくれよ。』と。
また、私の高校の頃の数学教師がこんなことを言っていました。
『ベクトルの足し算・引き算なんてのは、ただ2つの数がペアになっているだけなんだから、こんな簡単なことは算数で教えてほしい』と。当時の私は、『なにを言っているんだ、この人は笑』と思いましたが、いま振り返ると、確かに一理あるな、と少し思います。
これらを踏まえると、単に具体的・抽象的というだけでは、一歩踏み込み足りない気がします。今あげた二つの例は確かに、具体的かつ簡単な計算です。抽象的な数学(*2)という感じはしません。
ここで、考えるべきは寺子屋時代から伝わる"読み・書き・そろばん"という素晴らしいお言葉です。日常生活に必要な最低限の素養を端的にまとめた素晴らしい言葉ですが、この"日常生活"が算数を理解するキーワードです。
マイナスもベクトルも日常生活を送るうえで、全く意識する必要がありません。もちろん、あれば便利に越したことはないですが。
例えば、マイナス5℃と聞いて、『寒いんだな』と感じればそれ以上のことは全く必要ないですし、所持金3,000円で5,000円のものを買いたいときに、『5,000円-3,000円で2,000円足りないな』と思えば十分です。『3,000円-5,000円でマイナス2,000円足りてるな』と考える風変わりな人はめったにいないと思います。
つまり、算数とは、"日常生活に登場する程度の問題について、式が立てられて計算できる能力"を培う場と言えます。
(*1)中学受験をされていた都会の方は違うかもしれませんが、私のような田舎者はそもそも中学受験という概念がなく、何の変哲もない公立中学校で、数学になり初めて学んだのは、教科書通りの"正負の数"でした。
(*2)その後に続く議論が抽象的、例えば、マイナス×マイナスがプラスになるとか、内積の概念とかがあるから指導のしやすさの都合でしょ?という、理由はもちろんあると思いますが、本質的な理由でないので、今回はそこで議論を止めることはしません。
第5章『私の考える数学リテラシー』
さあ、"日常生活"というキーワードが登場したところで、いよいよ"数学リテラシー"について考えましょう。
まず、私が、『数学ができないんですよ』という相談を受けた場合、その相談者の課題は大きく3つに分かれると思っています。
第一に、"計算能力"。これは、単にルールに基づいて処理をする能力です。例えば、「因数分解が苦手で...」と相談してくる中高生(*3)はこれに該当します。
第二に、”数学コミュニケーション能力"。ここが今回の要です。そもそも数式とは言語なのです、それも世界共通の。
例えば、
"I have a pen."
ほぼすべての日本人が、こちら↑の文章の意味が分かると思います。
では、
".عندي قلم"
こちら↑の文章はいかがでしょうか?多分、読めないと思います。私も読めません。
内容自体は"I have a pen."をアラビア語(*4)で書いただけですが、私も含め皆様方は、ペンを知らないわけでも、持っているという状態が分からないわけでもないはずです。
ただ単に、アラビア語が分からないから、そもそも何が書いてあるのかが意味不明である、という状態かと思います。
数学においても、これと同じ状態が頻発します。数学が苦手だ、と言っているが、数理的素養があるかないかが分かる以前に、数学の言語が読めていない。そもそも書いてあることの意味が分からないので、考えることもままならない、といった状態です。意外と、ここで躓いている人は多いものです。
ちなみに、大学の二次試験では、ここの能力を意外と重視していて、難しい問題であれば、問題文を数学の言葉で書き直す、もしくは、数学の言葉で書かれている問題を日本語で書き直す、といった翻訳作業のみで、部分点が発生するケースもあります。
第三に、"証明する力"です。数学といえば、これです。これをやらずに数学とは言えませんし、実際、数学科(*5)における大学院まで合わせて6年間のほとんどはこれに費やされます。適切に定義をし、確かな論理を適切に積み重ねて、万物不変の正しさを示す作業です。
証明は純粋数学の醍醐味である一方で、"いったい何の役に立つの?"と言われてしまうのも、また事実。そんな時、私は『100年後の未来で役に立つかもしれないことをやるのが数学だよ』と答えるようにしています。
(*3)因数分解が苦手と相談された場合は、ほぼ確実に「500問以上の演習はしたか?」と尋ねます。ルールに基づいて処理するだけなので、適性により習熟の速さに多少の誤差はありますが、基本的にはスポーツと同じで、それが適正なものであれば、単純なトレーニングで身に着きます。
(*4)Google翻訳で雑に訳しただけなので、間違っていてもご容赦ください。
(*5)数学科には、高校までの数学(具体的には、数学Ⅲ・Cまで)を大学の証明を行うための基礎的な計算技術を学ぶ場ということを指して、"算数"と呼ぶという悪しきジョークがありました。私はあまり好きな言い回しではなかったですが、うまいこと言うな、とも思っていました。
第6章『数学リテラシーのホップ・ステップ・ジャンプ』
さて、前章で数学を構成する3要素を見てきました。
この章では、身に着けるべき数学リテラシーを語るうえで、習熟レベルについて語っていこうと思います。
習熟レベルは、シンプルに「分かる・使える・活用する」の3段階です。
例えば、上のイラストのような豚肉を見かけたとしましょう。
この時、自分で計算はしないが、会計で336円(480円:割引144円)と書かれたレシートを見て、そうだよね、と思えるのが"分かる"、値札を見た瞬間に、"480円×0.7=336円"だよな、と計算できるのが"使える"、430円の20%引きの魚とどっちが安いかを自分で検討できるのが"活用する"です。
上の例は簡単なので、"活用する"まで行ける方は多いと思いますが、もっと高度な計算や数学コミュニケーション、証明になった場合はどうでしょうか?
"分かる"とは、計算であれば、既に与えられている結果・答え、数学コミュニケーションや証明であれば、書かれている内容について理解できることです。英語でいうと、"リーディング・リスニング"の能力ですね。
"使える"とは、問題が与えられた場合、適切に計算したり、適切な数学コミュニケーションや証明の力を用いて、解決する力です。英語でいうと、"ライティング・スピーキング"の力ですね。
”活用する”とは、自分で新しい問題を見つけ、それに対して"使える"武器を組み合わせて、適切に解決を試みる能力です。上二つが、問題解決の"武器"とすれば、これは"戦闘スタイル"ともいうべき、より実践的な力ともいえるでしょう。
第7章『数学の世界で話してみれば...』
さて、数学コミュニケーション能力を"活用"できるレベルで習得しているとはどういうことでしょうか?この章では、そちらを少し捕捉します。
例えば、こちらの式↑を見てどう感じるでしょうか?
まず、『x?y?数字じゃなくて文字が出てくるとわけわかんない!』となるのは、数式が"分からない"人ですね。
では、この式を"分かる"人はどうでしょうか?
例えば、『一次関数だね、傾きは3で、切片は2。』など、この式に関する情報がいくつか出てくると思います。
では、"使える"人はどうでしょうか?
『まず、yは何で、xが何かを教えんかいっ!』と、私ならそう思います。
この一次関数を解析すればいいのか、それとも何かの関係式なのか、これだけでは全然分かりません。
先ほどの"I have a pen."構文で考えましょう。英語が"分かる"人は、これを見て、ペンを持っている人物が思い浮かぶと思います。しかし、実生活でこれを言われても、『見りゃ分かるわい!』となること間違いなしです。
英語を"使える"とは、"その場面で適切に使える"ことです。数式とてそれと同じです。
"使える"までいけば、"活用する"まであと一歩です。
がある量xとyがシンプルな直線の関係にあることを伝えるもの、という感覚があれば、xの部分がxの2次式になろうが、変数の数が2つ、3つと増えていこうが、単回帰分析の話になろうが自然にすんなり受け入れることができます。これが"活用する"です。
第8章『あなたの課題に狙いを決めて数学リテラシー』
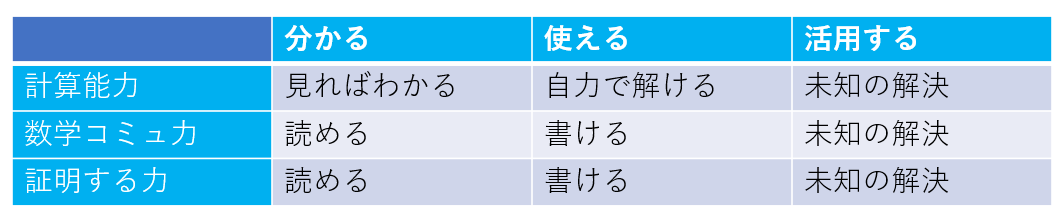
さて、前章までの数学リテラシーマップをまとめるとこんな感じです。
そして、私がすべての人に必要と考える数学リテラシーの範囲がこちらです。
どうです?意外でしたか?基本的に計算結果を出されて、それを、ふむふむ、とできる程度の能力があれば、大半の人は事足ります。
では、なぜいま数学リテラシーが必要なのでしょうか?
ここで、"日常生活"というキーワードが再登場します。"金融リテラシー"や"デジタルリテラシー"という言葉が台頭してきたのは、金融(特に資産形成)やデジタル(特に、スマホやAI)が無視できないレベルで、日常生活に関わってくるようになったからです。
なので、数字と触れ合う場面が多くなり、必要な計算能力の範囲が広がったわけですね。
それでは、"金融リテラシー"を積極的に身に着けたい方はどうするのがいいでしょうか?少なくとも、1級FPを取得した経験から申し上げると、未知の問題に対しても、しっかりと計算できる力を伸ばすことが大切です。金利の計算も、貯蓄運用のシミュレーションも、相続における分割や税制優遇の計算も所詮、割合と四則演算です。あとは、期待値という名の加重平均が計算できればもっと問題ありません。いずれも基本的な計算スキルの組み合わせなので、未知の問題に活用できるほどの計算能力があれば、金融リテラシーサイドからは問題ありません。(*6)
最後に、数学を学びたい、という全ての方へ。
伸ばすべき方向性は、数学コミュニケーション能力です。先にも述べましたが、数学は言語です。それも、自然界の謎を解き明かすために最適化された言語です。その言語が自由に使えれば、特に"デジタルリテラシー"分野を学ぶときに、不自由は大幅に減ります。その上、数式という構造化に長けた言語で物事を考えることができるので、ロジカルシンキングや新規に全く新しく学ぼうと思った場合も、数学コミュニケーション能力がとても役に立ちます。計算能力が実践に即使える能力とすれば、数学コミュニケーション能力は能力全般の底上げに役立つとでもいうべきでしょうか。
そして、証明する力はリテラシーとしてはほぼ必要ありません。ロジカルシンキングの礎としては最高ですが、ロジカルシンキングを学べば済む話です。もちろん、数学を6年間学んだ身としてしては、証明は面白いので、その趣深さが世の中に伝わると嬉しいですけどね。
長い間お付き合いいただきありがとうございます。
微積分やら行列やらは、各論にすぎません。計算能力を身に着けているのか、数学コミュニケーション能力を高めているのか、はたまた証明をしっかりしようとしているのか、に注目しながら、自己研鑽に励むことで、皆様の人生において数学が一層の輝きを放つことを心からお祈りします。
(*6)当たり前ながら、クオンツや、証券アナリスト、アクチュアリーなどの金融専門職を志す場合は、数学コミュ力が活用できるまであることはもちろん、証明する力まであると、尚良いです。