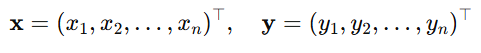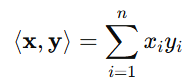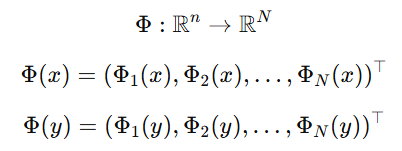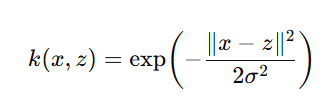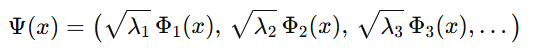こんにちは!
1級FP技能士のアシまるくんと申します。
第1章『さっぱり分からん!』
G検定・E資格の学習を進める中で、"カーネルトリック"という単語が登場しました。
概要としては、"カーネル関数"を用いて計算量を抑える数学的なテクニックです。が、これを見たときに、「そもそもカーネル関数って何なのか?」、「なぜ線形非分離問題が扱えるのか?」、「要約した計算量でうまくいくのはなぜなのか?」など溢れんばかりの疑問が浮かんできました。
試験対策としては、サポートベクトルマシン(SVM)とセットで覚えておけば、なんとかなりましたが、このままにしておくのも気持ち悪い。
そんな折、近所の図書館で赤穂先生の"カーネル多変量解析"という書籍と出会いました。
貸借期間である3週間のうち、融通がつく時間に読み進めましたが、やはり隙間時間で読めるほど簡単な内容ではない。しかし、自分なりにカーネルトリックについて理解した内容について、自分の"理解の最前線"(*1)として自分の言葉でまとめてみようと思います。
(*1)あくまで理解の最前線です。数学修士卒なので分かりますが、正しい数学の議論としては不十分極まりないです。今回はざっくり理解を主眼にしたので、ご容赦ください。
第2章『地図を見るより散歩をしよう』
まず、SVMとカーネルトリックの話の肝は、より高い次元に情報を移すことで簡単に分離ができるようになる、ということです。
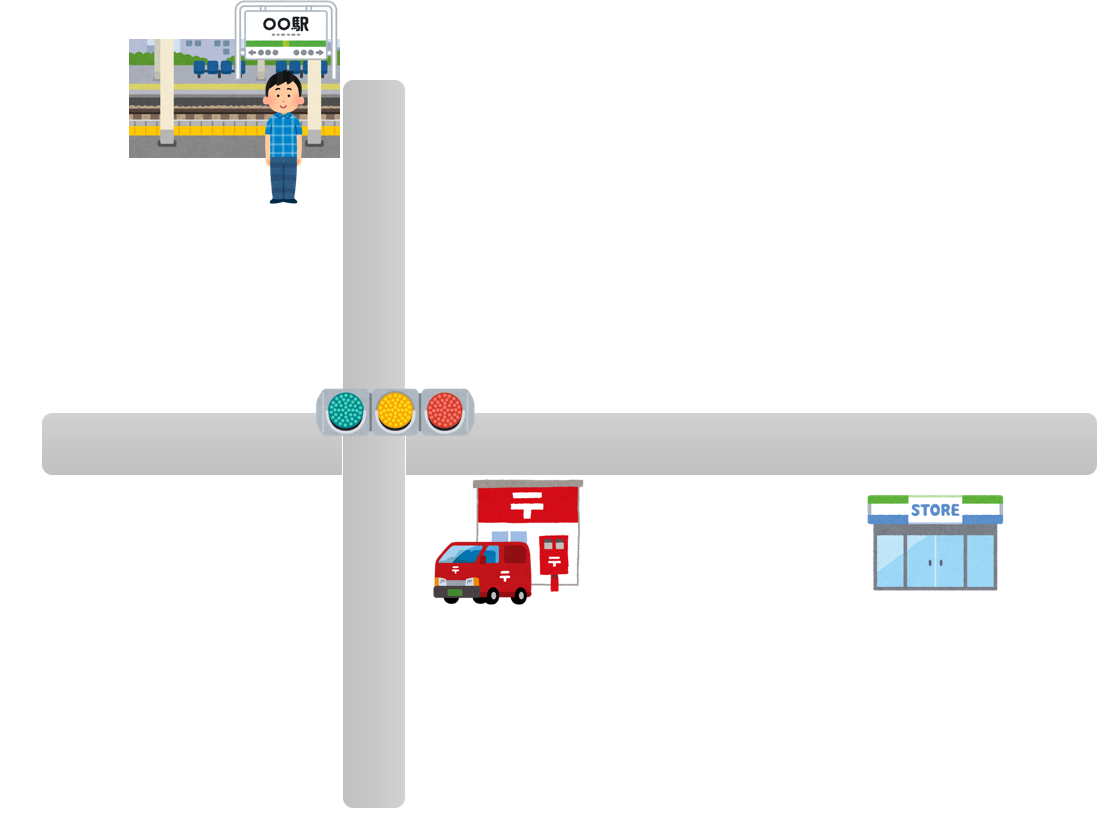
例えば、こちらの簡単な地図をご覧ください。いま駅にいて、郵便局に用事があるとします。この地図だけ見ると、「郵便局まで行くなら、ついでにコンビニも行こうかな」という気分になります。
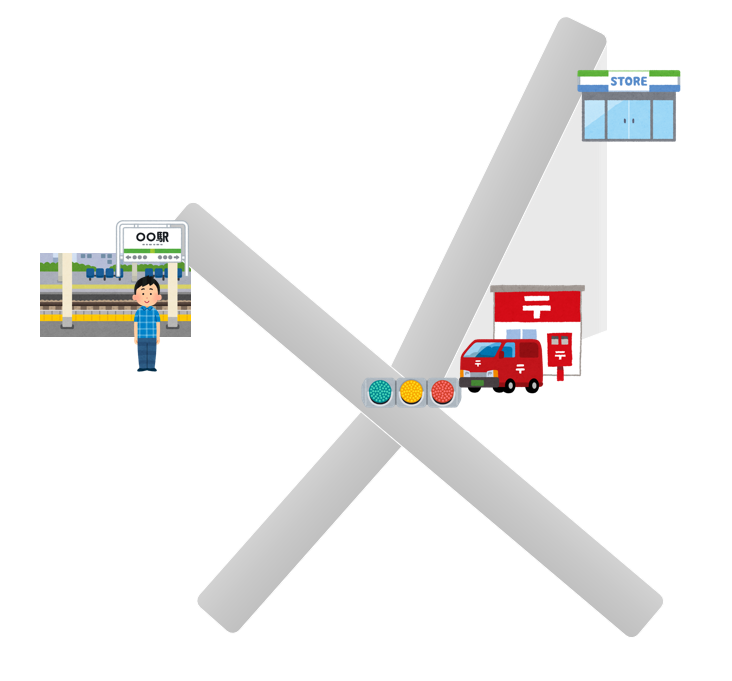
では、同じ地図を見取り図風に加工したものです。これを見た瞬間に、郵便局のついでにコンビニに行こう、という気持ちは消えてなくなると思います。つまり、地図という2次元の世界から実際の3次元の世界(*2)に移動すると、郵便局とコンビニの間に、"坂の上と下"という明確な分かれ目が生まれることに気付くのです。
これはとても身近な例ですが、データの世界でもこれと同じようなことをやることで、データを簡単に、ちゃんとした用語を使うのであれば"超平面"で分けましょう、というのがSVMとカーネルトリックの話のモチベーションです。
(*2)地図の世界から、現実の世界に移して考える場合など、移した後の世界のことを"特徴空間"と呼びます。
第3章『情報量を圧縮しよう』
では、高次元に気軽にホイホイと移行してよいのか、というお話です。"次元の呪い"という言葉がある通り、高次元になるにつれて計算量が膨大に増えていきます。この問題を解決するために登場するのが、"カーネル関数"です。
もっとも簡単なカーネル関数である、有限次元ベクトルの初等的な内積を考えましょう。
それぞれn次元ベクトルx,yに対して、内積は
と定めることができます。
つまり、この例では、もともと2n個あった情報がたった1個にまとまっています。この情報量の圧縮をもうちょっと一般的に拡大したものが"カーネルトリック"の考え方です。
もう少し丁寧に話をすると、
入力データ(前章の例でいうと2次元の地図上のデータ)
これを特徴空間に移した後の姿(前章の例でいうと現実世界での姿)
この2N個の情報量を1個にまとめる。これをカーネル関数と呼びます。
この内積が持つ"正定値性"(*3)という性質を持ついくつかの関数がカーネル関数として知られています。有名なものは、以下のガウシアンカーネルです。こちらは"無限次元の内積"と解釈することもできます。
(*3)正確には"半正定値性"ですが、正定値性という言葉が使われることも多いです。
第4章『知識と経験のエロス』
前章まで見てきたのは、高次元空間に移す⇒内積をとる⇒カーネル関数として情報が要約される、という流れでした。しかし、カーネルトリックにおいては、高次元空間を扱わずに計算量を減らす、という話でした。つまり、前章までで見たように高次元空間からカーネル関数を導き出すことなく、ポンと与えられたカーネル関数だけを見たときに、それ自体に高次元空間に相当する情報が内包されている必要があります。
以下の"Mercerの定理"から、カーネル関数が高次元空間を内包していることを感じ取ることができます。
Mercerの定理より、ここで、
とおけば、
となり、正定値性を満たすカーネル関数が何かしらの高次元空間ベクトルの内積で記述できることが分かります。これが、情報が要約されたカーネル関数だけ見れば、高次元空間の代わりになりうる下支えとなっているわけですね。
ここでポイントなのは、Mercerの定理は、カーネル関数が何らかの高次元空間の内積として表せることを保証していますが、その"高次元空間の構造までは担保していない"ということです。だからこそ、状況に合わせて適切なカーネル関数をチョイスするのは経験値がなせる業、まさに"知識と経験のエロス"なわけですね。