先日行われた「合格者の会 2022」の中で、松尾先生の講演の中に出てきた「過学習の先にある世界、Double Descent」について簡単に調べてみました。

会場で聞いたときは「過学習になっても、更にエポック数を増やしていけば、再びtest errorが下がる」･･･という事だと思っていましたが、もう少し奥が深かったようです。



🧿Double Descentとは


おそらく、以下の論文がオリジナルだと思われます。
https://arxiv.org/abs/1912.02292

これまで、モデルが複雑になるほど過学習（学習データに特化しすぎて、実際のデータに対する汎化性能が低下してしまう状態）が起きやすくなる･･･と言われており、過学習を防ぐために、ドロップアウトや正則化（ペナルティ）の追加、過学習の傾向が見られ始めたら学習をストップさせるアーリーストッピングなどで対策が行われてきました。

しかし、ある一定数以上のパラメータを持つ大規模なモデルであれば、「過学習の先に、再びTest errorが減少する（つまり、再度、汎化性能が向上し始める）」現象が見られるという内容です。

モデルの汎化性能向上（Test errorの減少）が、「学習のスタート時」と「過学習の後」の2回発生する･･･という事から、「Double Descent」と呼ばれているようです。

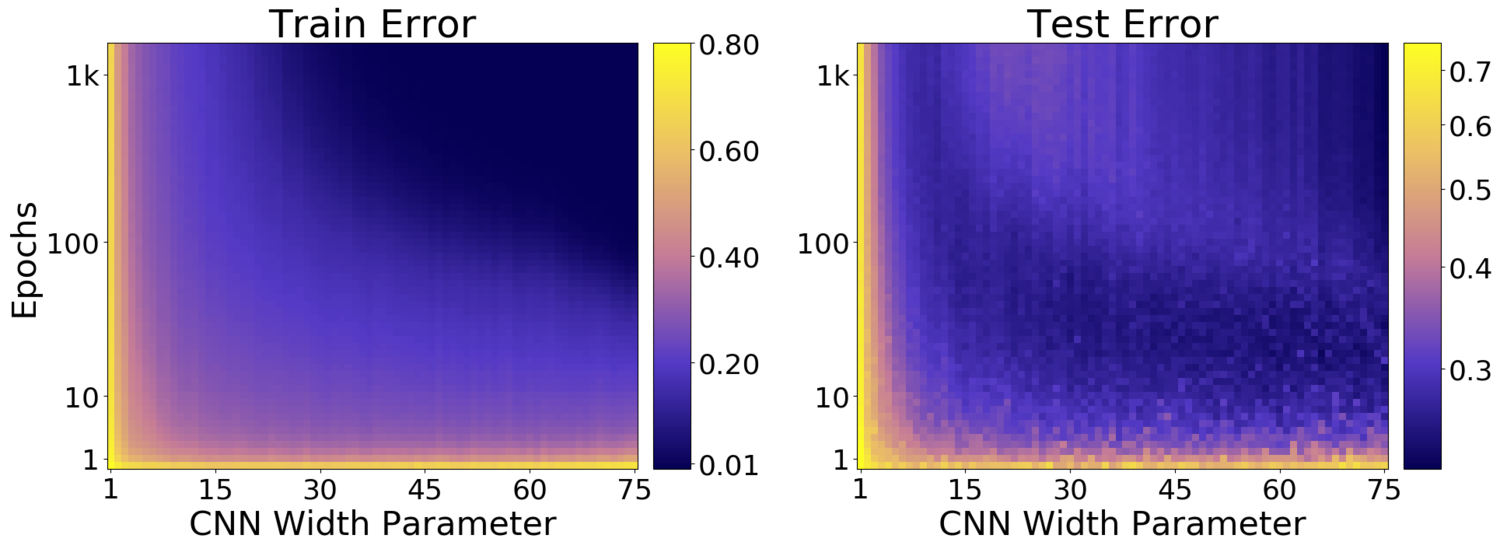
cnn-sgd-ocean.png 87.16 KB論文から引用（DEEP DOUBLE DESCENT: WHERE BIGGER MODELS AND MORE DATA HURT、Figure 25 より引用）した図ですが、左がTrain Error（つまり学習用データに対するエラー）、右側がTest Error（テスト用データに対するエラー、つまり汎化性能に直結する部分）になっています。
横軸は「CNNのパラメータの幅」、縦軸はエポック数になっており、色が寒色系になるほどErrorが少ないことを表しています。

まず、Train Errorの方を見れば、基本的には「エポック数が増えていけば、Errorも少なくなっていく」ことが分かります。（パラメータ数が極端に少ない場合は、学習が進まない状態も見て取れますが･･･）つまり、エポック数を増やしていけば「学習用データ」に対しては、どんどん学習が進んでいくことが分かります。

それに対して、「実際に利用する時の汎化性能」に直結するTest Errorですが、Train Errorとは少し様子が異なります。
注目すべきポイントが、一定パラメータ数以上のモデルであれば、エポック数が増えるにつれて「Errorが減少→増加→再び減少している領域が存在する」ことです。
この部分こそ、「Double Descent」が発生している部分ですね。



🧿エポック数だけじゃない！


この現象は「エポック数を増やせば発生する事象なんだな･･･」と思ってしまうかもしれません（私も最初はそう思っていました）が、実は「エポック数以外」の要因でも発生するようです。

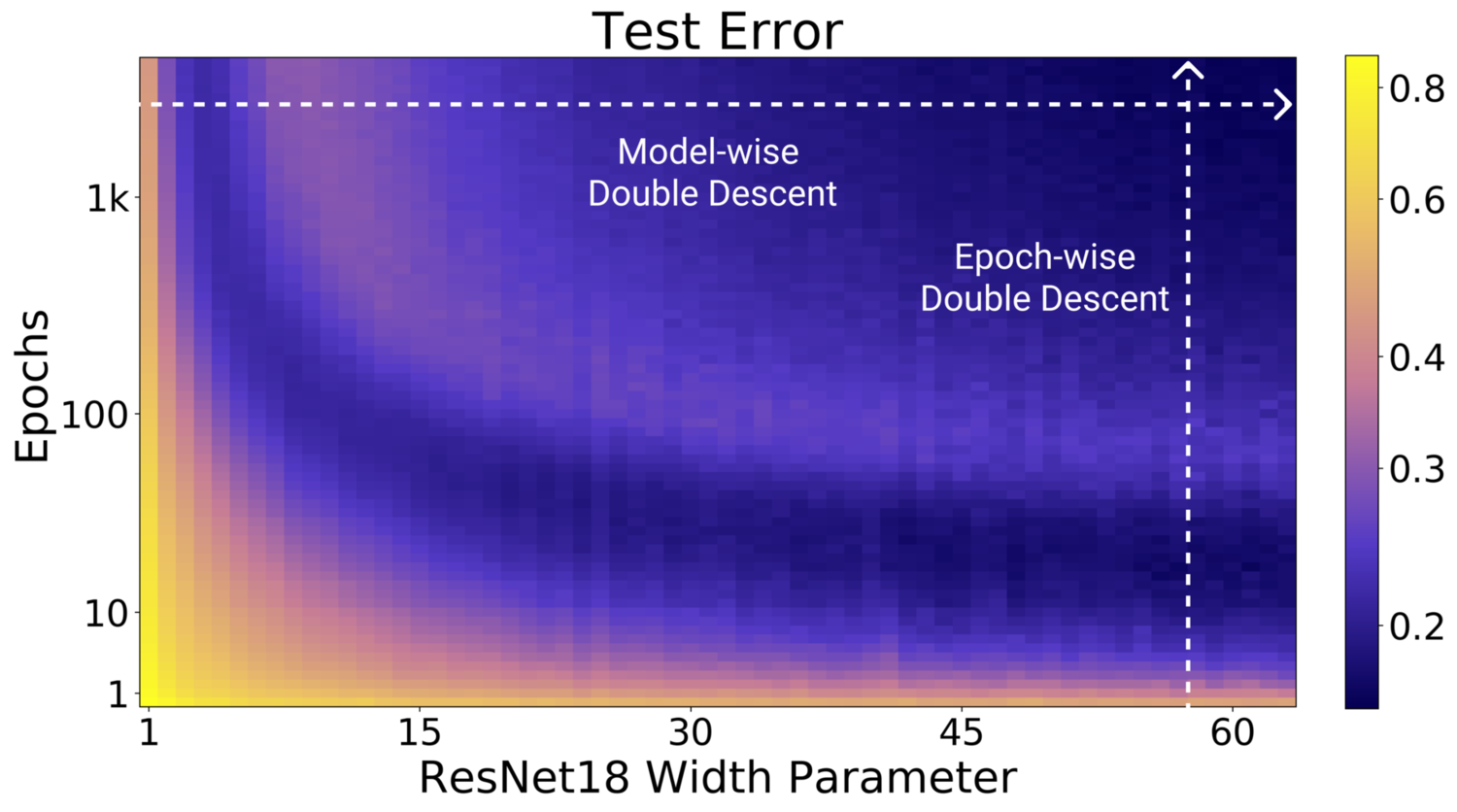
論文では、「Model-wise」、「Epoch-wise」と表現してありますが、「同じエポック数だったとしても、モデルのパラメータ数を増やしていく過程の中で、Double Descentが発生する」という事です。
Intro-ocean-test.png 206.71 KB論文からの引用（DEEP DOUBLE DESCENT: WHERE BIGGER MODELS AND MORE DATA HURT、Figure 2 より引用）ですが、横方向への矢印が「モデルのパラメータ数によるDouble Descent」、縦方向の矢印が「エポック数によるDouble Descent」を表しています。



🧿どういうときに発生するのか？


論文を斜め読みした感じでは、Double Descentには「いくつかの発生条件がある」ようです。

現在のところ、CNN、ResNet、Transformerなどで、正則化やアーリーストッピングを使わない場合に、このDouble Descentが発生するようです。また、モデルのパラメータ数の違いによっても、発生有無や、発生し始めるエポック数に違いが見られるようです。

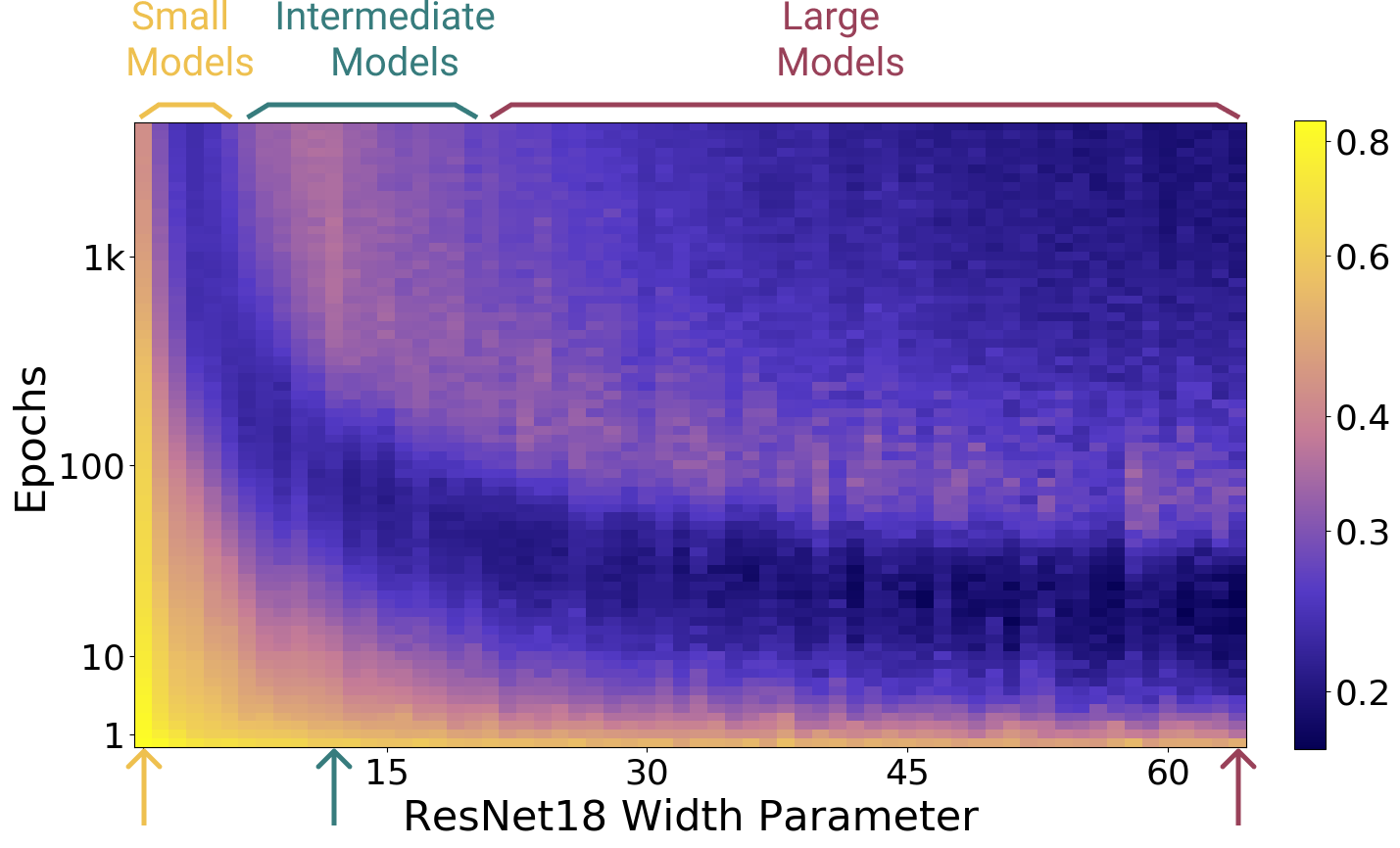
以下の図表（DEEP DOUBLE DESCENT: WHERE BIGGER MODELS AND MORE DATA HURT、Figure 9 より引用）は、ResNet18モデルのパラメータ規模を「小、中、大」の3つに分けて、各モデルでエポック数を増やしていったときに「Test errorの値がどう変化するか」を表した物になります。（図中の矢印やラベルの色と、グラフの色が対応しています）


epochDD_ocean_plot.png 82.02 KBepochDD_regimes.png 65.77 KB

Test Errorのグラフ（下の方のグラフ）を見れば分かるのですが、モデルの規模が小さい場合は、「Test Errorの値はエポック数とともに減少はするものの、十分に低い値にはならない（アンダーフィット）状態」になります。

モデルの規模が中くらいの場合は、「途中から過学習状態になり、その後もErrorは減少しない」感じになっています。このグラフは、多くの人がイメージする「過学習」のグラフに最も近いのではないでしょうか。

そして、モデルの規模が大きくなった場合、「過学習でTest Errorの値が悪化した後、再び減少に転じる、Double Descentが発生」しています。



🧿まとめ


このように、一般的に言われていた「モデルの規模が大きくなるほど過学習が起きやすい」という通説は、必ずしもそうではなく、「一定規模以上のモデルであれば、過学習の後にTest Errorが再び減少するケースもあり得る」という事になりますね。

このような現象が発生する明確な理由などはよく分かっていないようなので（現時点だと仮説段階？）、興味があればオリジナルの論文などを読んでみてください。