対角化の公式を思い出す方法

本日のおしながき

・はじめに
・対角化の公式を導出する流れ
・① → ② 固有値・固有ベクトルの計算を「列」に押し込める
・③ 対角行列を「右から掛ける」ことの意味
・まとめ
・(参考) 対称行列Aの固有ベクトルを並べて作成した行列は直交行列
・(参考) 対角行列を「左から掛ける」ことの意味

はじめに

E資格シラバス2022では完全に消え去っていた線形代数が、新シラバス「シラバス2024」で復活します。筆者もそれに合わせてシラバスに沿った記事執筆を再開しており、先日は「固有方向」の概念を知ることによって、固有値、固有ベクトルの計算方法をより確実に覚える方法を提案いたしました。

シラバス2024では、固有値、固有ベクトルの次が「対角化」です。本稿では、意外と覚えにくい対角化の公式を思い出しやすくなる方法を提案しようと思います。

全然難しくはありませんので、G検定に合格してこれからE資格にチャレンジしようと考えている皆様、およびE資格を取得したけど、対角化の式はすっかり忘れてしまったよという皆様(意外と多い、かも)にご一読頂ければ幸いです。

対角化の公式を導出する流れ

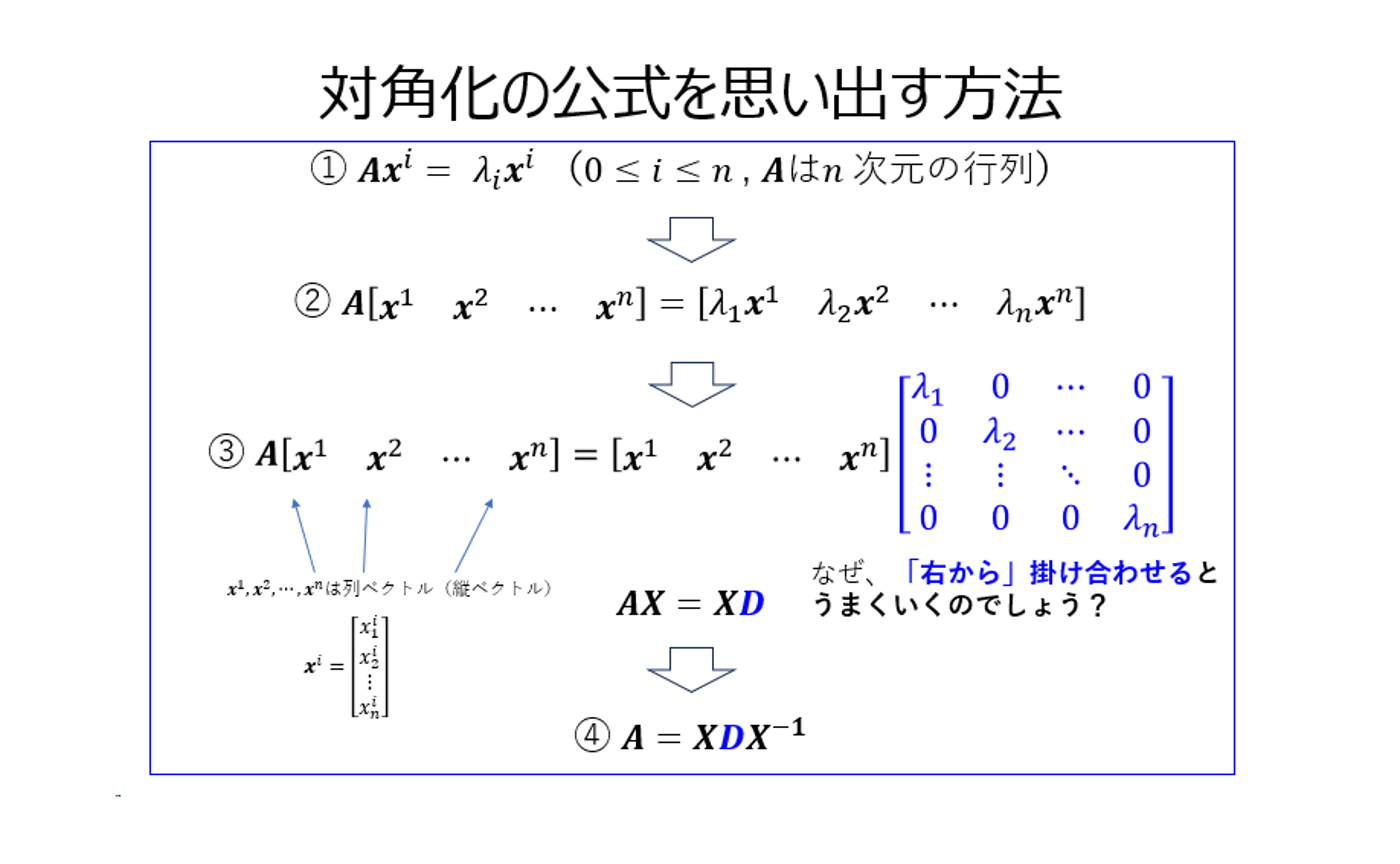
まずは全体の流れです。本稿のタイトル画像と同じです。
image.png 27.6 KB①～④を解説すると以下のようになります。
試験会場で対角化の式を思い出せなくなった場合の手順ですw

① 固有値・固有ベクトルの式を思い出す。キーワード「固有方向」を手掛かりに頑張って下さい！
② 固有ベクトルを列ベクトル(縦ベクトル)として横に並べる行列の式を作る
③ 固有値を対角成分に持つ対角行列を「右から掛け合わせる」式に変形する
④ ②で作った行列の逆行列を「右から掛け合わせる」式にすれば完成

ポイントは③の、固有値を対角成分に持つ対角行列を「右から掛け合わせる」箇所。これさえ思い出せれば、④において、逆行列が右に配置されることを確実に思い出せます。

ではここから順に、②、③を導出する過程を確認していきたいと思います。

① → ② 固有値・固有ベクトルの計算を「列」に押し込める

まずは①から②への変換です。
image.png 5.11 KB
この式で注意しておくべきことがひとつあります。それは、②の左辺、右辺ともに「 n × n 行列」であることです。決して横長ではありません。image.png 25.74 KB
でも、なぜ固有ベクトルを横に並べてうまくいくのでしょうか？それは大雑把にいうと以下の通りです。

個々の固有値・固有ベクトルの計算を、各列に押し込めることができるから

では、導出過程を見てみます。赤枠の場所を中心に押さえていきましょう。image.png 56.33 KB
でもどうして、赤枠の式は成り立つのでしょうか？１列目を例にとって確認してみましょう。まず、固有値・固有ベクトルの式を変形すると以下のようになります。image.png 19.36 KB次に、計算押し込めを狙った行列XOの式を変形すると以下のようになります。要はゼロ成分のおかげで、１列目以外の計算結果はゼロになるのです。image.png 21.15 KB(a)と(b)を比較すると、以下がわかります。image.png 9.48 KB
このように赤枠の部分を導出できれば、行列演算の線形性を利用して、以下のように②を導出できます。image.png 71.58 KB

③ 対角行列を「右から掛ける」ことの意味

次は②から③への変換です。image.png 19.03 KBこれは「対角行列を右から掛けると、各列ベクトルの対角成分倍を算出できる」という性質を利用しています。以下の図は、2列目に、２列目のベクトルを２個目の対角成分倍したベクトルが保存される様子を示しています。image.png 36.29 KB
まとめると、以下のようになります。

１列目の計算では１個目の固有値と１列目の固有ベクトルのみが掛け合わされる
２列目の計算では２個目の固有値と２列目の固有ベクトルのみが掛け合わされる
・・・
ｎ列目の計算ではｎ個目の固有値とｎ列目の固有ベクトルのみが掛け合わされる

まとめ

① 固有値・固有ベクトルの式さえ思い出すことができれば、あとは以下の手順で比較的容易に対角化の式を思い出すことができます。

② 固有ベクトルを列ベクトル(縦ベクトル)として横に並べる行列の式を作る
③ 固有値を対角成分に持つ対角行列を「右から掛け合わせる」式に変形する
④ ②で作った行列の逆行列を「右から掛け合わせる」式にすれば完成

特に重要なのは③。対角行列を右から掛け合わることを思い出しましょう。その時に、本記事の「対角行列を右から掛け合わせる意味」がお役に立てば幸いです。そうすれば、④の操作で「固有ベクトルを横に並べて作成した」行列の逆行列を「右から掛け合わせる」ことを思い出すことができるでしょう。
image.png 31.28 KB